LEYES DE NEWTÓN:
Las
leyes de Newton, también conocidas como
leyes del movimiento de Newton,
[1] son tres principios a partir de los cuales se explican la mayor parte de los problemas planteados por la
mecánica, en particular, aquellos relativos al
movimiento de los cuerpos.
Primera ley de Newton o Ley de la inercia
La primera ley del movimiento rebate la idea aristotélica de que un cuerpo sólo puede mantenerse en movimiento si se le aplica una
fuerza. Newton expone que:
Todo cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no ser que sea obligado a cambiar su estado por fuerzas impresas sobre él.
La segunda ley del movimiento de Newton dice que:
El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.[
En términos matemáticos esta ley se expresa mediante la relación:

Donde:
 es el momento lineal
es el momento lineal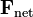 la fuerza total o fuerza resultante.
la fuerza total o fuerza resultante.
Suponiendo que la masa es constante y que la velocidad es muy inferior a la velocidad de la luz la ecuación anterior se puede reescribir de la siguiente manera:
Sabemos que  es el momento lineal, que se puede escribir m.V donde m es la masa del cuerpo y V su velocidad.
es el momento lineal, que se puede escribir m.V donde m es la masa del cuerpo y V su velocidad.

Consideramos a la masa constante y podemos escribir  aplicando estas modificaciones a la ecuación anterior:
aplicando estas modificaciones a la ecuación anterior:
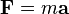
Tercera ley de Newton o Ley de acción y reacción
Con toda acción ocurre siempre una reacción igual y contraria: o sea, las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en sentido opuesto.


Equilibrio traslacional:
Un cuerpo se encuentra en equilibrio traslacional
cuando la sumatoria de todas las componentes en X es igual a 0 y todas las
componentes en Y es igual a 0.
Cuando un cuerpo esta en equilibrio traslacional no
tiene fuerza resultante actuando sobre el.
Primera Ley de Equilibrio:
Un cuerpo se encuentra en equilibrio si y sólo si la suma vectorial de las fuerzas que actúna sobre el es igual a 0.
|

Fx=Ax+Bx+Cx+Dx.......=0
Fy=Ay+By+Cy+Dy.......=0
|
ejemplo:
Una pelota de 300N cuelga atada a otras dos cuerdas, como se observa en la figura. Encuentre las tensiones en las cuerdas A, B Y C.

SOLUCIÓN:
El primer paso es construir un diagrama de cuerpo libre:

Al sumar las fuerzas a lo largo del eje X obtenemos :
S Fx = -A cos 60° + B cos 40° = 0
Al simplificarse por sustitución de funciones trigonométricas conocidas tenemos:
-0.5A + 0.7660B = 0 (1)
Obtenemos una segunda ecuación sumando las fuerzas a lo largo del eje Y, por lo tanto tenemos:
(Cos 30° + cos 50° )
0.8660A + 0 .6427B = 300N (2)
En las ecuaciones 1 y 2 se resuelven como simultanea A y B mediante el proceso de sustitución. Si despejamos A tenemos:
A = 0.7660 / 0.5
A = 1.532B
Ahora vamos a sustituir esta igualdad en la ecuación 2
0.8660(1.532B) + 0.6427B = 300N
Para B tenemos:
1.3267B + 0.6427B = 300N
1.9694B = 300N
B= 300N / 1.9694
B= 152.33N
Para calcular la tensión en A sustituimos B = 152.33 N
A = 1.532(152.33N) = 233.3N
La tensión en la cuerda C es 300N , puesto que debe ser igual al peso.
Equilibrio rotacional:
Es aquel equilibrio que ocurre cuando un cuerpo sufre un movimiento de rotacion o giro, al igual que el equilibrio traslacional debe tambien equilibrarse; surge en el momento en que todas las torcas que actúan sobre el cuerpo sean nulas, o sea, la sumatoria de las mismas sea igual a cero.
EMx= 0
EMy= 0
friccion o rozamiento:
La fricción o rozamiento es una fuerza que se presenta cuando
dos cuerpos se mueven uno respecto a otro. Es una fuerza que siempre se opone al
movimiento.
La formula para calcular la fuerza de friccion es...
Ff=N x μ
Ff = Fuerza de friccion
N = Fuerza Normal al plano de movimiento
μ = (miu) Coeficiente de fricción. El cual depende de los materiales en rozamiento.
Fuerza de fricción estática.
Existe una fuerza de fricción entre dos objetos que no están en movimiento relativo. Tal fuerza se llama fuerza de fricción estática. En la siguiente figura aplicamos una fuerza F que aumenta gradualmente, pero el bloque permanece en reposo. Como en todos estos casos la aceleración es cero, la fuerza F aplicada es igual y opuesta a la fuerza de fricción estática Fe , ejercida por la superficie.
Para ver el gráfico seleccione la opción "Descargar" del menú superior.
La máxima fuerza de fricción estática Fe max , corresponde al instante en que el bloque está a punto de deslizar. Los experimentos demuestran que:
Fe máx = m eN
Donde la constante de proporcionalidad se denomina coeficiente de fricción estática. Por tanto, la fuerza de fricción estática varía, hasta un cierto límite para impedir que una superficie se deslice sobre otra:
Fe máx <= m eN
Fuerza de fricción cinética
En la siguiente figura mostramos un bloque de masa m que se desliza por una superficie horizontal con velocidad constante. Sobre el bloque actuán tres fuerzas: el peso mg , la fuerza normal N, y la fuerza de fricción Fk entre el bloque y la superficie. Si el bloque se desliza con velocidad constante, la fuerza aplicada F será igual a la fuerza de fricción Fk.
Para ver el gráfico seleccione la opción "Descargar" del menú superior
Podemos ver que si duplicamos la masa m, se duplica la fuerza normal N, la fuerza F con que tiramos del bloque se duplica y por tanto Fk se duplica. Por tanto la fuerza de fricción cinética Fk es proporcional a la fuerza normal N.
Fk = m k N
La constante de proporcionalidad m k es un número sin dimensiones que se denomina coeficiente de fricción cinétic.
 
Trabajo:
En física, se entiende por trabajo a la
cantidad de fuerza multiplicada por la
distancia que recorre dicha fuerza. Esta puede ser aplicada a un punto
imaginario o a un cuerpo para moverlo. Pero hay que tener en cuenta también, que
la dirección de la fuerza puede o no coincidir con la dirección
sobre la que se está moviendo el cuerpo. En caso de no coincidir, hay que tener
en cuenta el ángulo que separa estas dos direcciones.
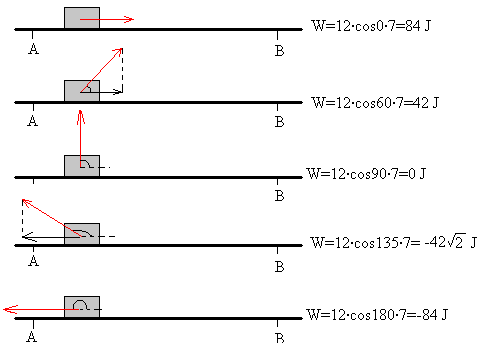
T = F. d. Cosα
Por lo tanto. El trabajo es igual al producto de la fuerza por la distancia y
por el coseno del ángulo que existe entre la dirección de la fuerza y la
dirección que recorre el punto o el objeto que se mueve.
Trabajo mecánico: Es igual al producto de la componente de la fuerza en la dirección del movimiento del cuerpo por la distancia que recorre el cuerpo. Es una cantidad escalar. W=Fd o W=(Fcos0)d W=trabajo F=fuerza d=distancia Unidades de trabajo Kpm=kilopondímetro J=joule J=Nm=0.102 Kpm 1Kpm=9.81 J Nm=newton x metro.
Potencia: Es el cociente de dividir el trabajo realizado por una fuerza entre el tiempo empleado en realizarlo. P=Watt W=J t=s v?m/s P=W/t=Fd/t=Fv
EJEMPLO DE POTENCIA:
Calcular la potencia que genera el trabajo realizado por una fuerza de 80N en 30m, durante 50s. P=? W=? F=80 N t=50 s d=30 m P=Fd/t=(80 N)(30 m)/50s=48 W W=Fd=(80 N)(30 m)=2400 J
Energía:
Es la capacidad de un cuerpo para realizar un trabajo. Sus unidades son: 1 Joule = kg m2/s2 = 0.238 cal 1 cal 4.186 J I Btu = 60.2 J
|
|
es el momento lineal
la fuerza total o fuerza resultante.
es el momento lineal, que se puede escribir m.V donde m es la masa del cuerpo y V su velocidad.
aplicando estas modificaciones a la ecuación anterior:


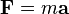





Muuy buena informacion Arbe...keee buenoo ke pones atencion a clasees jajaj!
ResponderEliminarjejjej a claro !! yo siempre creo!! aii leve solo k es mucha teoria y pocas formulas.
ResponderEliminar